Tại sao những con số, những suy diễn có vẻ có lý lại dẫn chúng ta đến những nhận thức sai lầm, đó là những gì tác giả Jordan Ellenberg muốn giải thích qua quyển sách Để không phạm sai lầm.
Được sự đồng ý của alphabooks, Zing trích đăng cuốn sách này.
Câu chuyện này, như nhiều câu chuyện về Đại chiến Thế giới lần thứ hai khác, bắt đầu khi quân Đức Quốc xã săn lùng một người Do Thái ở châu Âu và kết thúc với sự hối tiếc của chúng về điều đó.
Abraham Wald sinh năm 1902 ở thành phố Klausenburg, bấy giờ thuộc Đế quốc Áo-Hung. Khi Wald còn là một thanh niên, Đại chiến Thế giới lần thứ nhất kết thúc và thành phố quê anh trở thành vùng Cluj, Romania. Là cháu nội một giáo sĩ Do Thái và con trai một thợ làm bánh cho người Do Thái, nhưng cậu thanh niên Wald đã là một nhà toán học ngay từ rất sớm.
Tài năng toán học của anh nhanh chóng được phát hiện, và anh được nhận vào học toán ở trường Đại học Viên, nơi mà anh bị thu hút vào các chủ đề trừu tượng và khó hiểu ngay cả theo các tiêu chuẩn của toán học thuần túy: lý thuyết tập hợp và không gian mêtric.
 |
| Nhà toán học thống kê Abraham Wald. |
Nhưng khi các nghiên cứu của Wald hoàn thiện vào giữa thập niên năm 1930, nước Áo vẫn chìm trong cơn kiệt quệ kinh tế, và không có cơ hội cho người nước ngoài trở thành giáo sư ở Viên. Một công việc từ Oskar Morgenstern đã cứu Wald. Morgenstern về sau đã nhập cư vào Mỹ và giúp phát minh ra lý thuyết trò chơi, nhưng vào năm 1933 ông là giám đốc của Viện nghiên cứu kinh kế Áo, nơi ông thuê Wald với một mức lương bèo bọt để làm các công việc vặt liên quan tới toán học. Điều này hóa ra lại là một bước đệm tốt cho Wald: kinh nghiệm trong lĩnh vực kinh tế giúp anh giành được học bổng tại Ủy ban Cowles, một viện kinh tế lúc đó được đặt ở Colorado Springs (Mỹ).
Bất chấp tình hình chính trị nước Áo ngày càng xấu đi, Wald vẫn lưỡng lự chưa quyết định đi một bước có thể khiến anh rời xa khỏi toán học thuần túy. Nhưng rồi việc Đức quốc xã xâm chiếm Áo giúp quyết định của Wald trở nên dễ dàng hơn đáng kể. Chỉ sau vài tháng ở Colorado, anh được mời làm giáo sư thống kê ở Columbia; anh lại đóng gói đồ đạc và lên đường tới New York.
Và đó là nơi anh tham chiến.
Nhóm nghiên cứu thống kê (SRG), nơi Wald dành nhiều thời gian trong Đại chiến Thế giới lần thứ hai, là một chương trình bí mật móc nối sức mạnh tổng hợp của các nhà thống kê Hoa Kỳ với các nỗ lực chiến tranh một thứ giống như Dự án Manhattan, chỉ khác là các vũ khí được phát triển ở đây là những phương trình chứ không phải chất nổ.
Và SRG thực ra lại ở chính Manhattan, nằm tại số 401 phía Tây phố 118 Morningside Heights, chỉ cách Đại học Columbia vài dãy nhà. Tòa nhà này giờ đây là khu nhà ở cho giảng viên Đại học Columbia và văn phòng của một số tiến sĩ, nhưng vào năm 1943 nó là trung tâm đầu não ồn ào và náo nhiệt của toán học thời chiến.
Tại Nhóm Toán học ứng dụng Columbia, hàng tá phụ nữ trẻ gò lưng bên những máy tính cơ Marchant tính toán các biểu thức để tìm quỹ đạo bay tối ưu cho máy bay tiêm kích sao cho luôn bám sát máy bay địch. Ở một tòa nhà khác, một nhóm các nhà nghiên cứu từ Princeton đang phát triển các quy trình đánh bom chiến lược. Và nhóm dự án bom hạt nhân của Columbia ở ngay phòng bên cạnh.
Nhưng trong số các nhóm này, SRG là nhóm có nhiều quyền lực nhất và có ảnh hưởng lớn nhất. Môi trường này là sự kết hợp giữa sự cởi mở và sức mạnh to lớn về trí tuệ của một cơ sở hàn lâm với ý thức chung về mục đích vốn chỉ xuất hiện trong những tình huống sống còn.
“Khi chúng tôi đưa ra các khuyến nghị”, giám đốc W. Allen Wallis viết, “thường thì mọi việc sẽ diễn ra như thế. Máy bay chiến đấu lao vào trận đánh mang theo súng máy trộn lẫn các loại đạn theo đúng khuyến nghị của Jack Wolfowitz và phi công có lúc trở về, có lúc thì không. Máy bay của hải quân phóng những quả tên lửa với lượng thuốc nổ vượt qua các kiểm định mẫu của Abe Girshick, và các quả tên lửa có thể sẽ phát nổ và tiêu diệt chính máy bay của chúng tôi cùng phi công hoặc cũng có thể sẽ tiêu diệt mục tiêu”.
Tài năng toán học của nhóm cũng tương xứng với tầm quan trọng của nhiệm vụ. Theo lời của Wallis, SRG là “nhóm những nhà thống kê lỗi lạc nhất từng được tổ chức, cả về số lượng lẫn chất lượng”. Frederick Mosteller, người sau này thành lập khoa thống kê của Harvard, từng là thành viên của nhóm. Cả Leonard Jimmie Savage, nhà tiên phong cho lý thuyết ra quyết định và người ủng hộ nhiệt thành cho lĩnh vực sau này gọi là thống kê Bayes cũng từng ở đó. Norbert Wiener, nhà toán học của trường MIT và là nhà sáng tạo ra điều khiển học, cũng tham gia nhưng không thường xuyên. Đây là nhóm mà Milton Friedman, nhà kinh tế học đoạt giải Nobel sau này, thường là người xuất sắc thứ tư.
Người thông minh nhất phòng thường là Abraham Wald. Wald từng là thầy của Allen Wallis ở trường Columbia và đóng vai trò người lãnh đạo về toán học của nhóm. Do vẫn là một “kẻ ngoại đạo” nên theo nguyên tắc Wald không được phép xem các báo cáo mật của mình; có một câu chuyện đùa trong nội bộ SRG rằng những người thư ký được lệnh giật các trang ghi chép ra khỏi tay ông ngay sau khi ông vừa viết xong.
Wald, ở một mức độ nào đó, là một thành viên không được trông đợi. Ông lúc nào cũng thiên về sự trừu tượng và xa rời những ứng dụng trực tiếp. Nhưng động cơ của ông về việc sử dụng tài năng để chống lại phe Trục là rõ ràng. Và khi bạn cần biến một ý tưởng mơ hồ thành toán học vững chắc, Wald là người bạn muốn có bên cạnh.
 |
| Máy bay chiến đấu lao vào trận đánh mang theo súng máy trộn lẫn các loại đạn theo đúng khuyến nghị của Nhóm nghiên cứu thống kê (SRG). |
Và đây là câu hỏi. Để giúp máy bay khó bị đối phương bắn hạ, ta sẽ tăng cường giáp cho nó. Nhưng lớp vỏ giáp khiến máy bay nặng hơn và chiếc máy bay nặng hơn thì khó di chuyển hơn và tốn nhiên liệu hơn. Bọc giáp quá nhiều là vấn đề; nhưng bọc quá ít cũng là vấn đề. Phương án tối ưu nằm đâu đó ở giữa. Lý do một nhóm các nhà toán học tập trung trong một căn hộ ở New York chính là để tìm ra cách tối ưu đó.
Quân đội đến gặp SRG với một vài dữ liệu họ cho là có thể hữu dụng. Khi các máy bay chiến đấu Mỹ quay trở lại sau khi tham chiến ở châu Âu, chúng bị phủ đầy các lỗ đạn. Nhưng sự hư hại không phân bố đều trên máy bay. Phần thân máy bay có nhiều lỗ đạn, còn ở động cơ thì không có mấy.
Các sĩ quan thấy một cơ hội nâng cao hiệu suất; có thể dùng ít giáp hơn mà vẫn bảo vệ được máy bay nếu tập trung lớp giáp ở những nơi cần thiết nhất, chính là nơi mà máy bay thường bị trúng đạn nhiều nhất. Nhưng chính xác là cần thêm bao nhiêu giáp cho các phần đó của máy bay? Đó là câu trả lời họ muốn khi tìm đến Wald. Nhưng câu trả lời mà họ nhận được lại hoàn toàn khác.
Lớp giáp, Wald nói, không cần dùng cho những nơi có nhiều lỗ đạn. Nó cần được bọc ở những nơi không có lỗ đạn: động cơ.
Sự sáng suốt của Wald đơn giản nằm ở việc hỏi: các lỗ đạn còn thiếu ở đâu? Các lỗ đạn đáng lẽ phải rải khắp trên vỏ động cơ, nếu các hư hại phân bố đều nhau trên toàn bộ máy bay? Wald khá chắc chắn là ông biết câu trả lời. Các lỗ đạn còn thiếu nằm trên các máy bay bị hạ. Lý do các máy bay quay trở về có ít lỗ đạn trên động cơ là vì những chiếc bị trúng nhiều đạn trên động cơ đã không thể quay trở lại.
Việc nhiều máy bay quay trở lại căn cứ với phần thân lỗ chỗ vết đạn là một bằng chứng mạnh mẽ rằng trúng đạn ở thân máy bay có thể (và do đó nên) chấp nhận được. Nếu đến phòng hồi sức cấp cứu, bạn sẽ trông thấy số người bị bắn ở chân nhiều hơn rất nhiều so với số người bị bắn ở ngực; đó là vì những người bị bắn vào ngực đã không thể nào qua khỏi.
Đây là một mẹo toán học cũ khiến bức tranh hoàn toàn rõ ràng: cho một vài biến số bằng không. Trong trường hợp này, biến số cần điều chỉnh là xác suất để một máy bay trúng đạn vào động cơ mà vẫn quay về được. Gán cho xác suất đó bằng không có nghĩa là lần trúng đạn duy nhất vào động cơ chắc chắn sẽ triệt hạ chiếc máy bay đó.
Như vậy thì dữ liệu sẽ trông như thế nào? Bạn có thể thấy những chiếc máy bay quay trở về với vết đạn 16 chỗ trên cánh, thân và mũi nhưng không có lỗ nào trên động cơ. Các nhà phân tích quân sự có hai phương án giải thích việc này: hoặc là đạn của người Đức bắn trúng tất cả các phần của máy bay trừ động cơ, hoặc là động cơ là tử huyệt của máy bay. Cả hai giả thiết đều giải thích cho dữ liệu đó, nhưng giả thiết thứ hai hợp lý hơn nhiều. Lớp giáp cần được bọc ở những nơi không có lỗ đạn.
Khuyến nghị của Wald nhanh chóng được áp dụng và vẫn còn được hải quân, không quân sử dụng trong chiến tranh Triều Tiên và Việt Nam. Tôi không biết chính xác bao nhiêu máy bay chiến đấu của Mỹ đã được cứu, mặc dù các chuyên gia phân tích dữ liệu thế hệ sau của SRG trong quân đội ngày nay hẳn nắm rõ. Các quan chức quốc phòng Mỹ biết rõ rằng bên thắng trận không chỉ nhờ vào việc gan dạ hơn đối phương hay được Chúa ưu ái hơn. Bên chiến thắng thường là những bên giảm được 5% số máy bay bị bắn hạ, hoặc tiết kiệm thêm 5% nhiên liệu, hoặc có thêm 5% lượng chất dinh dưỡng cho bộ binh với chỉ 95% chi phí. Đó không phải là những gì làm nên các bộ phim về đề tài chiến tranh, mà là những gì làm nên một cuộc chiến thực thụ. Và nơi nào toán học cũng góp mặt.
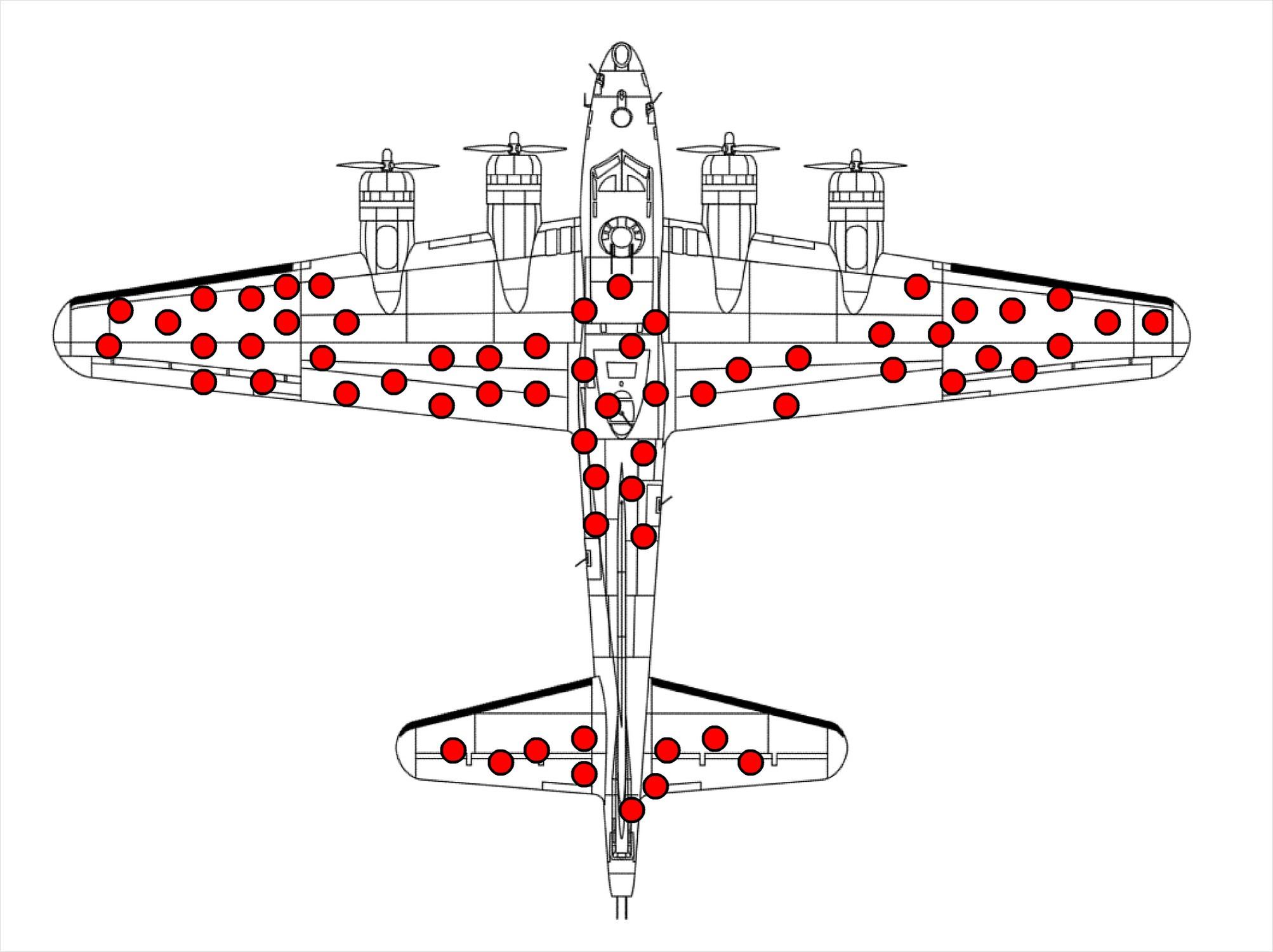 |
| Lớp giáp, Wald nói, không cần dùng cho những nơi có nhiều lỗ đạn. Nó cần được bọc ở những nơi không có lỗ đạn: động cơ. |
Tại sao Wald nhìn thấy điều mà các sĩ quan, vốn có kiến thức và hiểu biết vượt trội về không chiến, không nhìn thấy? Đó là nhờ thói quen tư duy được toán học đào luyện của ông. Một nhà toán học luôn luôn hỏi: “Bạn đang đặt ra những giả định nào? Và chúng đã thỏa đáng chưa?” Điều này có thể gây khó chịu. Nhưng nó cũng có thể rất hiệu quả.
Trong trường hợp này, các sĩ quan đang đặt ra một giả định vô thức: rằng các máy bay quay về là một mẫu ngẫu nhiên của tất cả các máy bay. Nếu giả định này đúng, bạn có thể rút ra kết luận về phân bố của các lỗ đạn trên tất cả máy bay bằng cách xem xét phân bố 16 đạn chỉ trên các máy bay sống sót. Ngay sau khi đặt ra giả thiết đó thì bạn chỉ mất một khoảnh khắc để nhận ra rằng nó hoàn toàn sai; không có lý do gì để kỳ vọng các máy bay có chung một khả năng sống sót như nhau bất kể chúng bị trúng đạn ở đâu.
Lợi thế khác của Wald là thiên hướng trừu tượng bẩm sinh. Wolfowitz, người từng nghiên cứu cùng Wald ở Columbia, viết rằng ông thích làm “những thứ trừu tượng nhất” và ông “luôn sẵn sàng nói về toán học nhưng không quan tâm đến việc phổ biến hay các ứng dụng đặc biệt”.
Bản tính của Wald khiến ông khó tập trung chú ý vào các bài toán ứng dụng. Các chi tiết của máy bay và súng trong mắt ông chỉ như lớp vỏ bọc, ông bị thu hút vào vấn đề toán học gắn kết với câu chuyện. Đôi khi, cách tiếp cận đó có thể bỏ qua các điểm then chốt. Nhưng nó cũng khiến bạn thấy bộ sườn chung của vấn đề vốn bề ngoài trông rất khác nhau. Nhờ vậy, bạn sẽ có kinh nghiệm hữu ích ngay cả trong các lĩnh vực mà dường như chẳng có chút kinh nghiệm gì.
Với một nhà toán học, cấu trúc ẩn sau bài toán lỗ đạn là một hiện tượng gọi là thiên lệch kẻ sống sót. Nó xảy ra hết lần này đến lần khác, dưới đủ mọi hoàn cảnh. Và khi bạn quen với nó, giống như Wald, bạn sẽ là người đầu tiên chú ý tới nó bất kể nó có lẩn trốn ở đâu.
( Còn tiếp)






























